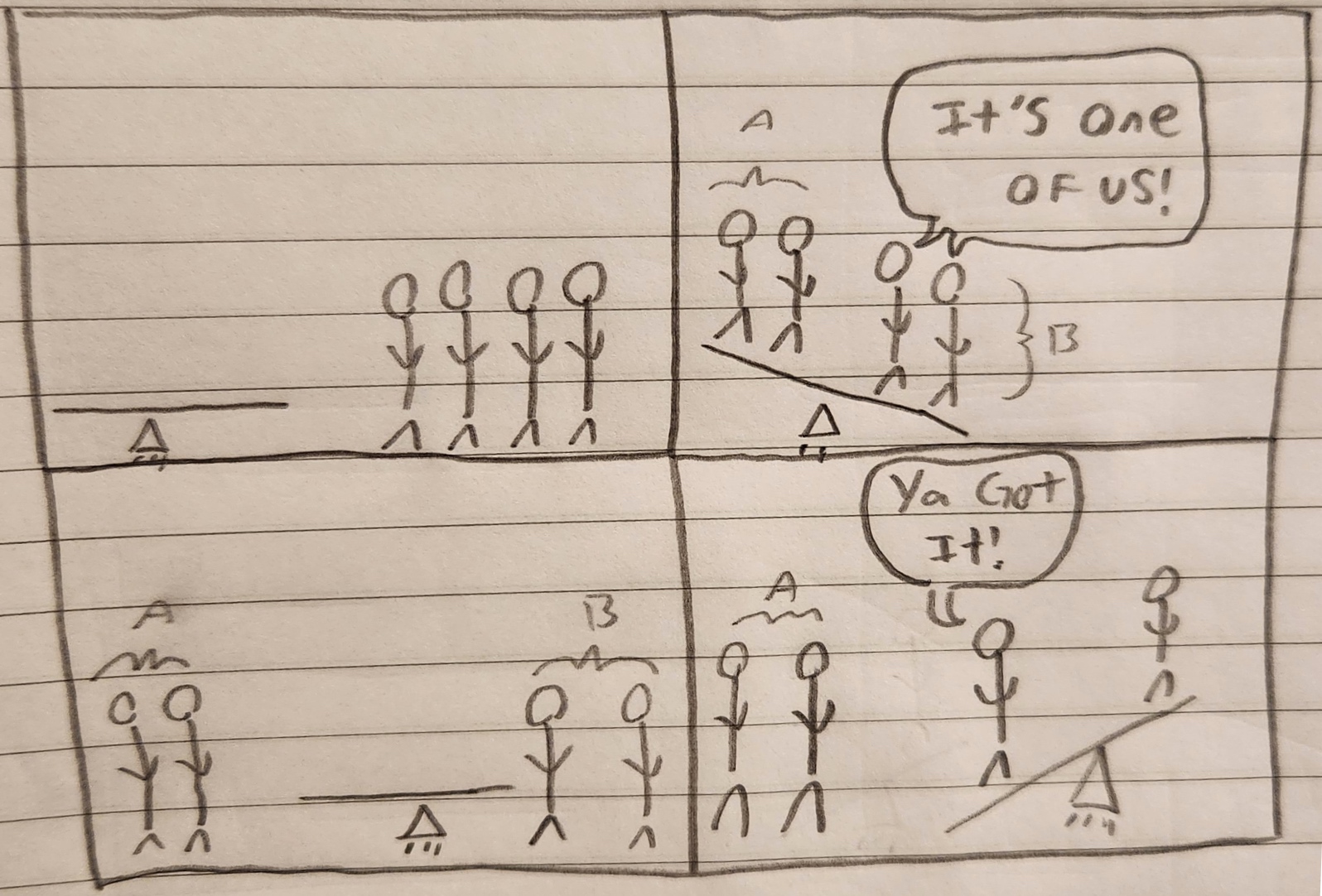"Those islanders and their pathetic seesaw haunt my dreams. They mock me in my sleep. Riding up and down in a teeter-totter of taunts."
- Captain Holt
In Season 2 Episode 18 of legendary sitcom Brooklyn Nine-Nine, Captain Holt presents his detectives with the following riddle:
There are 12 people on an island. Eleven of them are the same weight, but one weighs either more or less than the others.
How would you find out which one is the odd-one-out, and whether they are heavier or lighter, using only a giant seesaw which can
balance any number of islanders against each other? The catch is that you can only use the seesaw 3 times.
Insight #1: Don't try to solve the puzzle
Look, if you want to launch headfirst into solving this puzzle with 12 people and a heavier-or-lighter odd-one-out, go for it.
This is how the vast, vast majority of people will approach this, and a lot of them will solve it in a reasonable amount of time.
A lot of people might even solve it faster than we're going to solve it in this article.
That's fine, but it doesn't really interest me.
What interests me is learning how to solve puzzles, and deeply understanding them, so that I can solve other puzzles more easily too.
For reference, while writing this article, I challenged myself to solve the question "How many islanders could you sort out with 5 weighings, and what is the full step-by-step solution?"
It took me 13 minutes to figure out that it was 118 people and to sketch out a compact notation for all the steps in each case, and I just used a single side of an 8.5x11 paper. I think that's pretty good.
If you just want to see the solution, you can scroll down for it, or just google the problem and look at one of many articles or videos that go through it quickly.
We are going to start with the classic problem-solving approach of "try to solve a simpler version of the problem first", and we'll work our way up to the full problem (and beyond).
Simplification 1 - the odd-one-out can't be lighter
The odd-one-out is either heavier or lighter and we don't know which one it is. This feels pretty complicated. Let's get rid of that and say that we know they are heavier than the others.
Let's also quickly clarify - we don't know how much heavier they are. They might be heavier than four of the other people put together, they might weigh exactly as much as two others, they might weigh 5% more than one. We don't know, and can't use this information in any way.
This would be an interesting extension to the problem - what if you had a piece of information like "the odd one out weighs exactly as much as 2 other people"? But we're not going to go there today.
Simplification 2 - fewer people
We can also reduce the number of people.
Let's start with 2. I don't think anyone should have difficulty with this one:

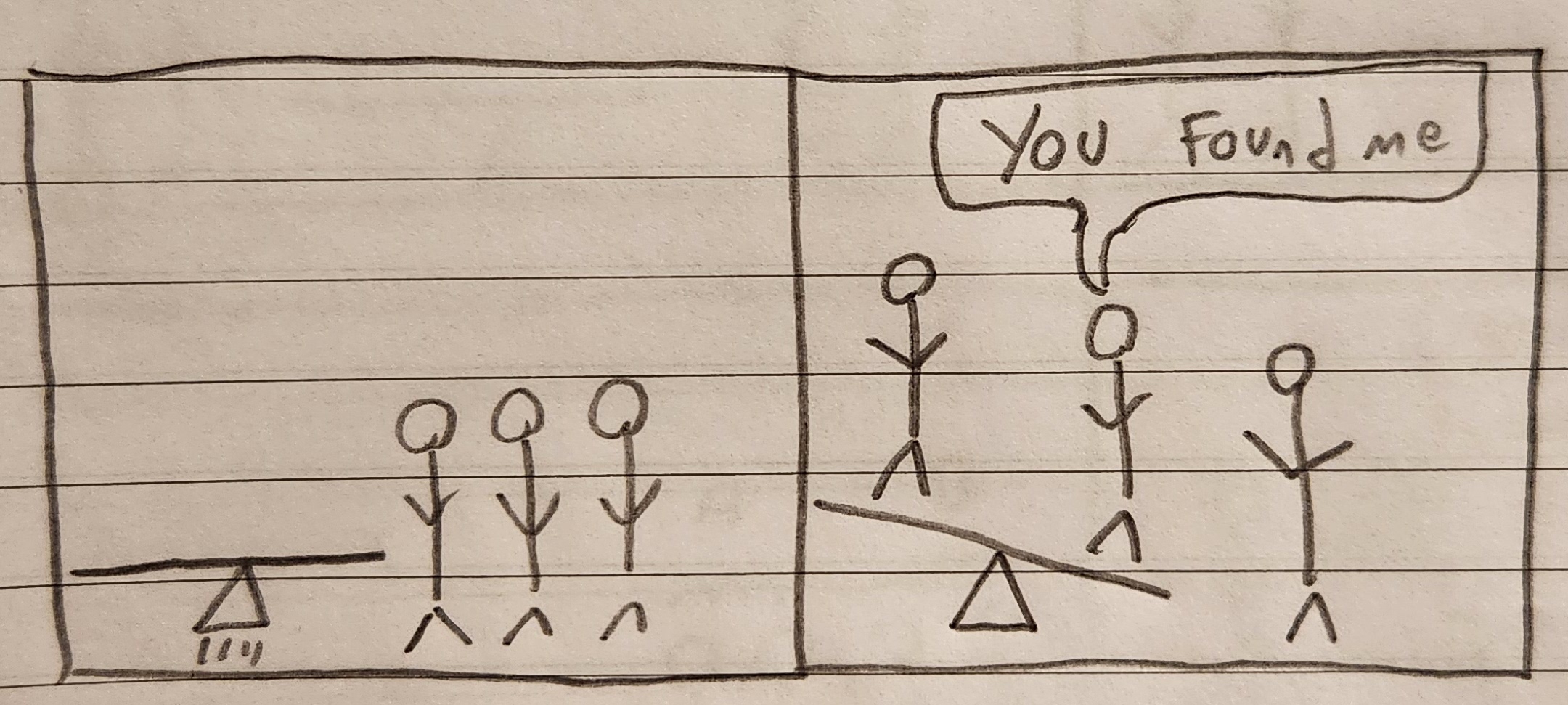
Great. Lets go one harder. Now there are three people, and one is heavier than the other two.
We could weigh them 1v1, with 1 person left out, or weigh them 1v2. 1v2 doesn't make any sense because if it tips to the side with more people, we learn nothing at all:

If we weigh 1v1, the seesaw might tip to one side and we found the heavier islander:
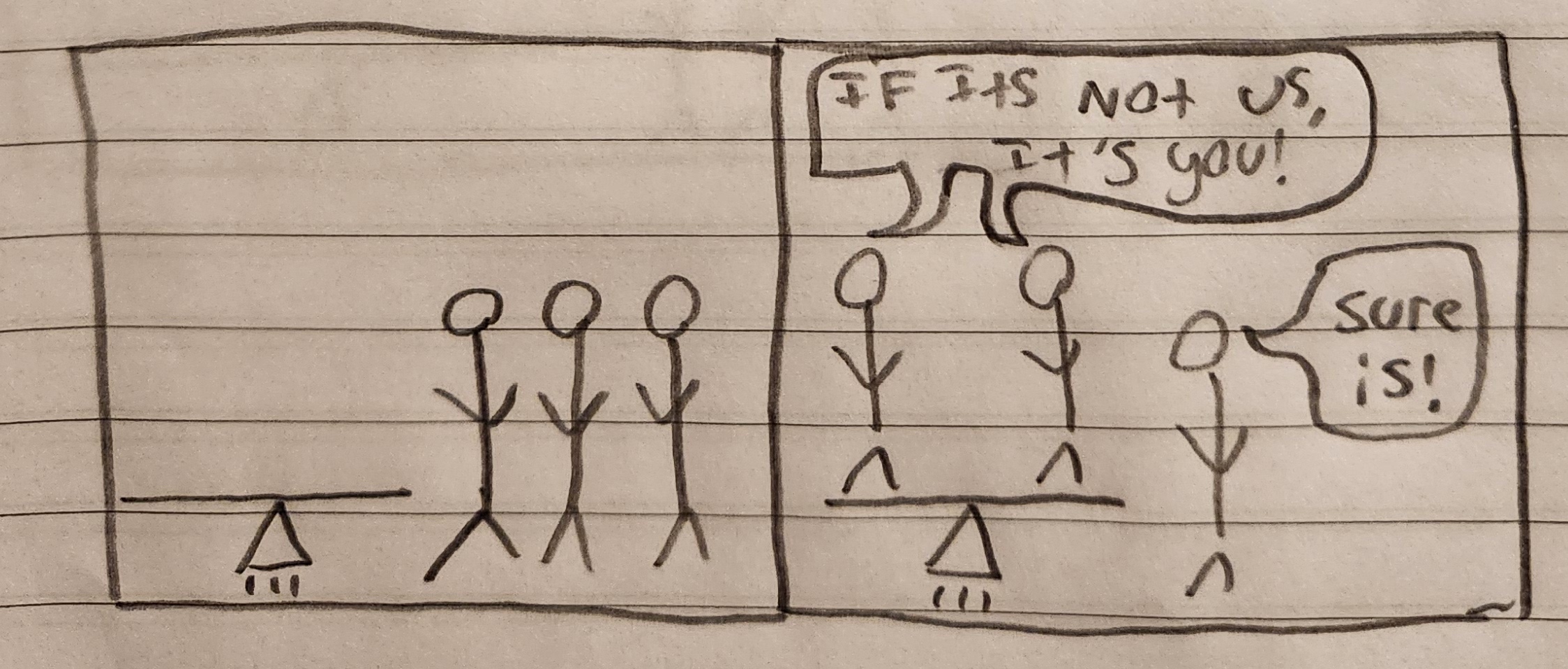
Or the seesaw might balance and then we know it must be the remaining person:
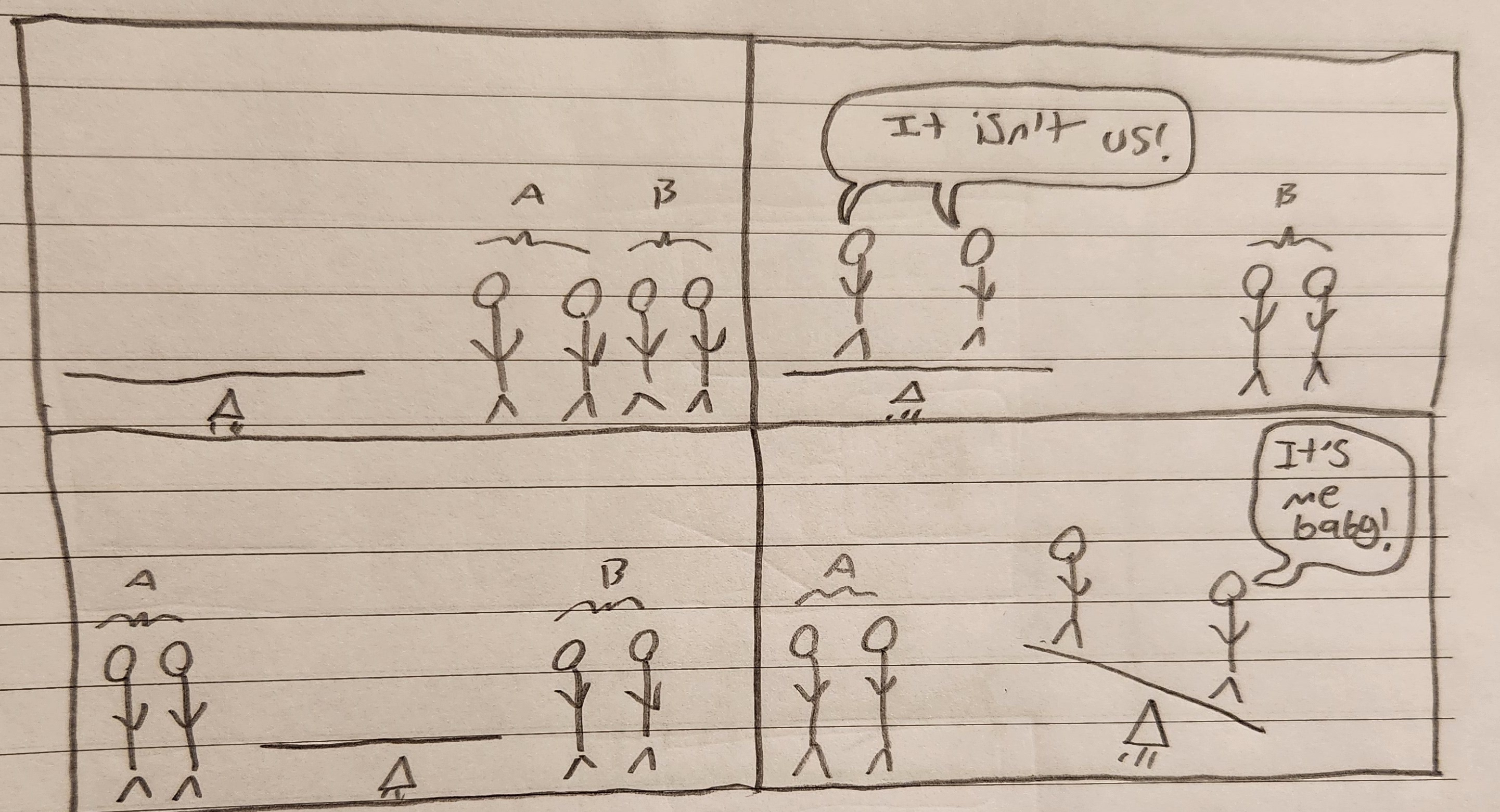
Okay. What if there were four people?
Well, we have two reasonable options. We could weigh 2 vs 2 or 1 vs 1.
If we do 2 vs 2, we know that one side will definitely have the heavier person, but we won't know which of the two people it will be.
We would have to take the two people on the heavier side and weigh them against each other to find the odd-one-out.
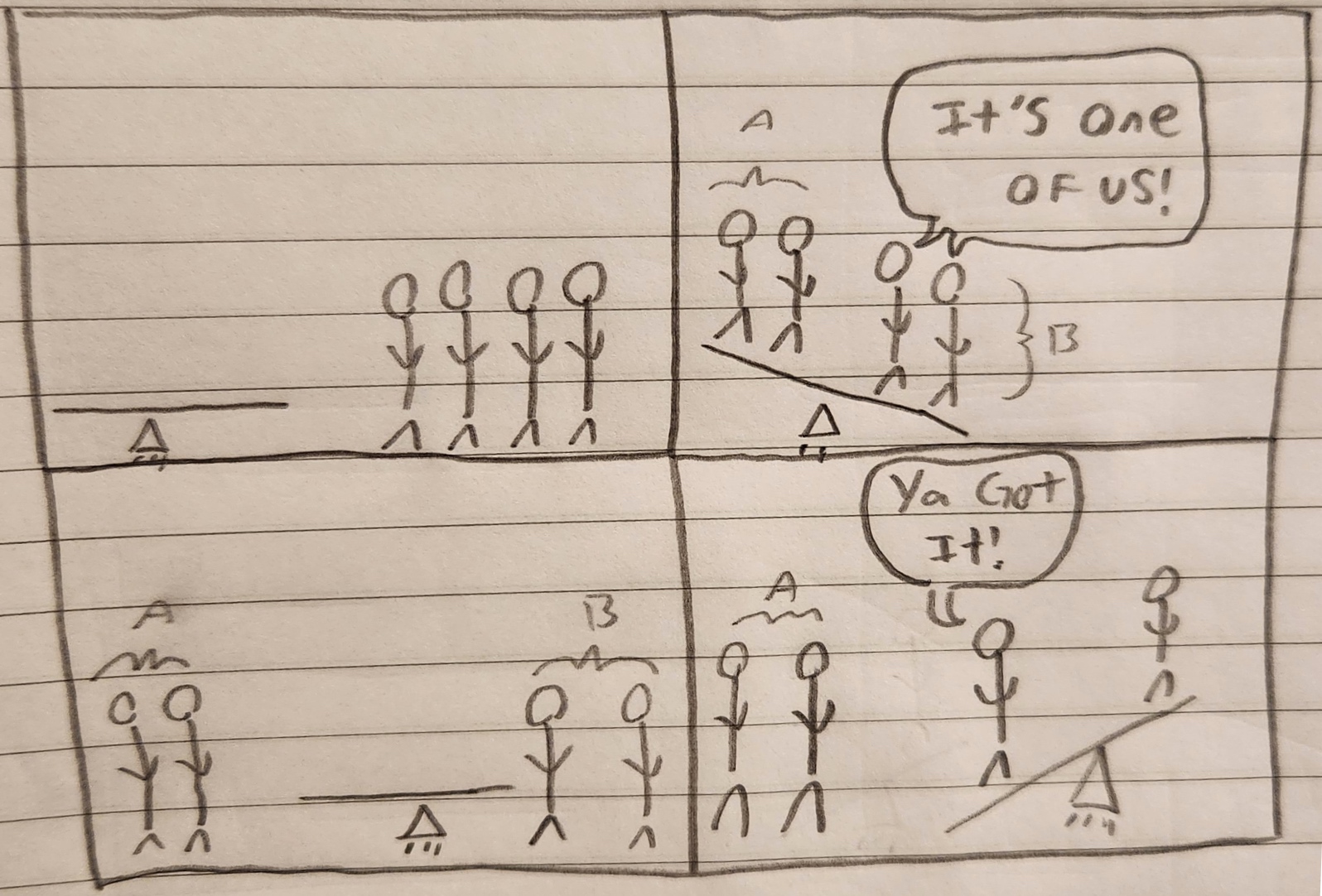
If we do 1 vs 1, we might find the person immediately (if the seesaw tips one way) but the seesaw might balance, and then we have two unknown people left, so we have to weigh those two against each other.
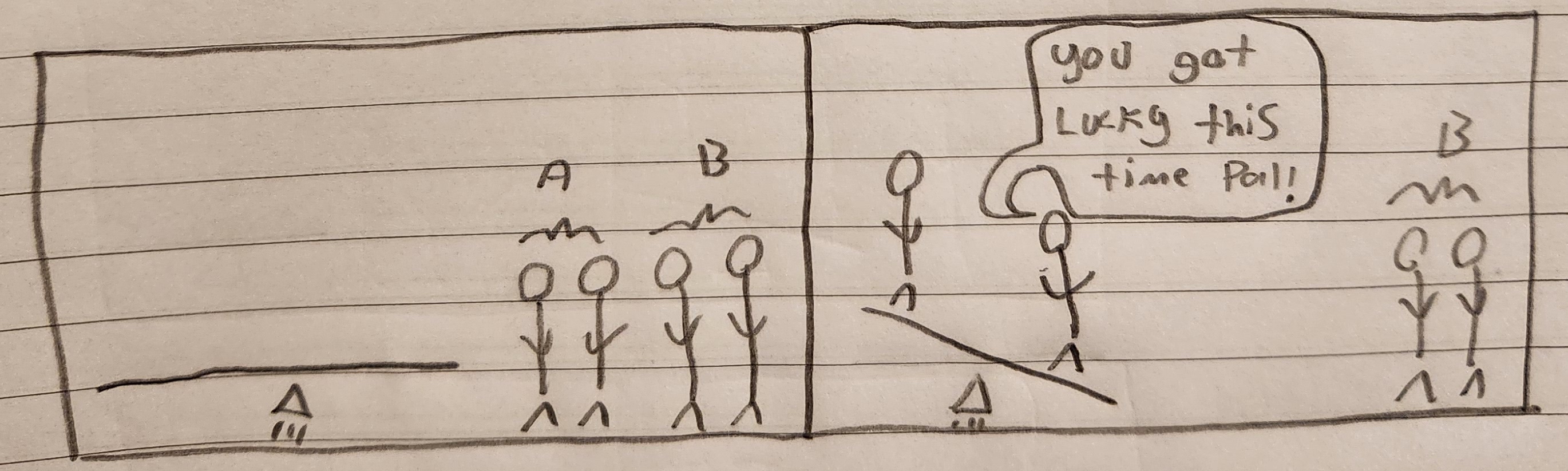
*yawn*. I'd love to ask about five people but this is getting a bit boring.
The good news is that I don't want to talk about five people either! It may not seem like it, but from our very simple examples we have already learned an ENORMOUS amount:
With two people, the seesaw is guaranteed to tip one way or the other, and we can find out who is heavier. But with three people, we were still able to solve it with just one weighing!
This was because the seesaw has a third possibility, which is that it might balance. And we saw that this is okay! We can also learn information from the seesaw if it balances,
and we don't need everyone to be on the seesaw for us to gain information about them.
We also saw that we cannot solve the four-person puzzle with a single use of the seesaw. Again, this is because the seesaw only has three possibilities: right-side-heavy, balanced, left-side-heavy.
It isn't just by chance that one weighing let us solve the three-person puzzle but not the four-person puzzle - it is a fundamental fact of the seesaw. With one weighing, it can distinguish between three possibilities.
Okay so if one use of the seesaw lets us solve a three-possibility-puzzle, what can we do with TWO uses of the seesaw?
We can definitely solve a six-possibility-puzzle, because three plus three is six, right?
Lets try it!
As fun as that sounds, here's an even better idea. We are going to take what we have learned so far and proudly shout from the rooftops:
"I can solve a six-possibility-puzzle with two seesaw-uses, and I'm so sure of myself that I'm not even going to TRY it!"
I wonder if we can do more than six? Let's try seven.
With seven people, we could weigh 1vs1, 2vs2, or 3vs3 to start. I think we can all agree that 1vs1 doesn't seem like the best use of our time.
If we weigh 2vs2, the seesaw might tip one way or the other, and then we will have to weigh the people on the heavier side against each other.
If the scale balances, there will be three people left, and we already solved the three-person-puzzle! So we can definitely do 7 people with just two uses of the seesaw.
Hmm. So 3+3=6, but we can actually solve even bigger problems with only two uses of the seesaw.
In fact, since we already know we can solve a 3-person-puzzle with one seesaw-use, we could add one more person to each side of our 7-person-puzzle.
Now, if it tips one way or the other, we take the 3 people on the heavier side into round 2, and if it balances it is the same as before.
Either way, we have three people to sort out in round 2, which we know we can do. We also know that we definitely can't solve a 10-person puzzle,
because then there would be an outcome with 4 people in round two, and we can't solve that with one seesaw-use.
diagram
Explanation of multiplication
Now we have a very clear rule:
With N seesaw-uses left, we can solve a problem with 3^N possibilities.
Let's go back to the original problem. There are 12 people. One of them is either heavier than the others, or lighter than the others.
Let's create some notation. An "HL" person is someone who we know nothing about: they might be the odd-one-out-heavy, they might be the odd-one-out-light, or neither.
An "L" or "H" person will be someone who we know is only a candidate for one of the possibilities.
For example, if we weighed 6 people against the other 6, the people on the heavy side will all become "H"s and the people on the light side will all become "L"s,
We know that if someone was on the light side of the scale, they can't possibly be odd-one-out-heavy, and vice-versa.
Finally, a "N" person will be someone who is known not to be the odd-one-out. For example, if the scale balances, then everyone on it is an "N".
N stands for "known". Fight me.
So in Captain Holt's problem, we start with twelve HLs:
HL
HL
HL
HL
HL
HL
HL
HL
HL
HL
HL
HL
Of these 24 Hs and Ls, only one of them is correct. Therefore, this is a 24-possibility-puzzle. Given our multiplication rule, 3*3*3=27, so we should be able to solve a 24-person puzzle with three seesaw-uses.
something about how we only want guaranteed results!
something about how it has to be nine.
Let's look at options for the first weighing: 6vs6, 5vs5, 4vs4, 3vs3, 2vs2, 1vs1
By the way, this is where most people start the puzzle. By launching in headfirst. If you can solve it this way in a reasonable amount of time, power to you.
But if you solved it this way, I have a challenge for you: you can use the seesaw five times. How many people could you solve this puzzle for, and what is the full solution? I did this on a piece of 8.5x11 paper (yes it was messy - but you could read all the answers) in less than 13 minutes.
Anyway. Let's get started. With 6vs6, we know the scale will tip one way or the other. As discussed earlier, this means the six people on the heavy side will become "H"s (candidates for being odd-one-out-heavy), and the six people on light side will become "Ls":
Hey! Remember when we solved the three-person-puzzle just as easily as the two-person-puzzle?
Those super boring super obvious examples? The whole point was to show that we can learn three things from the seesaw, depending on its three states.
If we weigh 6vs6, we know it will tip one way or the other, so we can only determine between two possibilities, not three! This is limiting how much we will learn!
This thinking, by the way, is totally correct. We don't even need to LOOK at 6vs6, because it is a sub-optimal choice.
With 5 vs 5, the seesaw will either tip or balance. If it tips, we will have:
N
N
H
H
H
H
H
L
L
L
L
L
If it balances:
N
N
N
N
N
HL
HL
N
N
N
N
N
If it balances, there are two unknown people, which is very easy to resolve with two seesaw-uses.
We could, for example, just weigh them against one of the "N" people, one at a time.
If it does not balance, we have 5 "H"s and 5 "L"s, which leaves us ten possibilities, which won't work, so 5vs5 is not the starting point.
I want to pause for a second here and review some of the problem solving strategies we have been using.
- We made much easier versions of the problem, and solved those first.
In fact, they were almost TOO easy, but by thinking about them deeply, we were able to understand fundamental concepts about how this puzzle works.
- We came up with a clear notation for organizing our work. Boooooring! But also super important. Remember what I was saying about we didn't even need to try 6 vs 6?
If we did try it, we would have this outcome:
[diagram]
Even without our fancy "multiply-threes" rule, it would be pretty clear at this point that 5vs5 is a better option than 6vs6 and we don't have to try 6 vs 6.
Note to self: it would be even better to just start by drawing the diagrams for all the starting options.
- Going a bit deeper, we realized that the best arrangements of people on the seesaw are the ones that have all three possible outcomes, (i.e. those that can tip or balance)
Alright lets look at 4vs4 and 3vs3. 3vs3 has 6 "HL"s if it balances, which is twelve possibilities, so it won't work.
4vs4 has 4 "HL"s if it balances, which is eight possibilities. If it tips, there will be four "H"s and four "L"s, which is eight possibilities.
We found our guy.
back